Binary Search Tree (이진 검색 트리)
- 노드는 모두 다 다른 키(value)값을 가져야 함
- 각 노드는 최대 2개의 자식을 가짐
- 모든 노드의 키(value)값은 다음 성질을 만족
- 자신의 왼쪽 subtree에 있는 모든 노드의 키보다 크다.
- 자신의 오른쪽 subtree에 있는 모든 노드의 키보다 작다.
Binary Search Tree의 시간 복잡도
| Array(배열, 정렬X) | Linked List | Array(배열, 정렬 O) | Binary Search Tree | |
| Search | O(n) | O(n) | O(log n) | O(log n) |
| Insert | O(n) | O(n) | O(n) | O(log n) |
| Remove | O(n) | O(n) | O(n) | O(log n) |
※ Insert, Remove의 경우는 임의의 위치에 삽입 삭제가 이루어진다고 가정
※ Linked List는 단방향 연결리스트라고 가정
Binary Search Tree - Traversal (순회)
- 시간 복잡도는 average case, best case, worst case 모두 O(n)
- Breadth-First Search (BFS) : 너비 우선탐색
- Level - order search (레벨순으로 탐색)
- Queue를 이욯해 구현
- 루트부터 시작, children node를 queue에 넣고 하나씩 꺼내서 방문. 꺼낸 노드에 대해 children node들을 다시 큐에 넣는 과정을 반복

- Depth-First Search (DFS) : 깊이 우선탐색
- Stack을 이용해 구현
- Root의 위치에 따라 Pre, In, Post로 나뉨.
- Preorder(전위) : <root> - <left> - <right>
- Inorder(중위) : <left> - <root> - <right> > 해보면 알겠지만 오름차순으로 정렬된 결과가 나옴
- Postorder(후위) : <left> - <right> - <root>
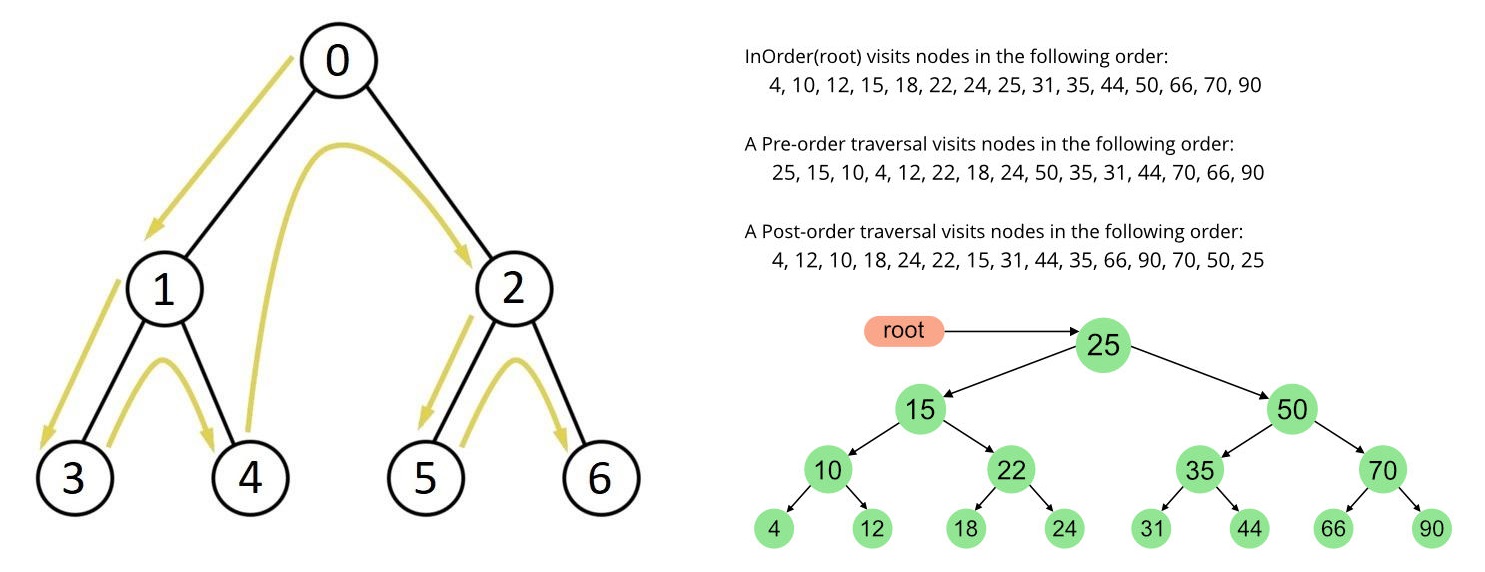
DFS가 그림으로 잘 표현된 사이트
- https://www.algotree.org/algorithms/tree_graph_traversal/pre_in_post_order/
Preorder, Inorder and Postorder tree traversals :: AlgoTree
Preorder, Inorder and Postorder tree traversals Tree traversal - The idea is to visit all the nodes of a binary tree using the connecting edges and print the data within each node based on the traversal technique. - Tree traversal algorithms begin the trav
www.algotree.org
'Python > 자료구조, 알고리즘' 카테고리의 다른 글
| 자료구조, 알고리즘) Graph - About Graph, DFS, BFS (1) | 2024.05.22 |
|---|---|
| 자료구조, 알고리즘) Sorting - Shellsort, Mergesort, Heapsort, Radixsort (1) | 2024.05.17 |
| 자료구조, 알고리즘) Sorting - Bubblesort, Selectionsort, Insertionsort, Quicksort + Partition (1) | 2023.12.10 |
| 자료구조) Binary Tree (4) | 2023.11.28 |
| 자료구조) Tree의 기본 개념 (3) | 2023.11.28 |