< Binary Search Tree ⊂ Binary Tree ⊂ Tree ⊂ Graph >
Binary Tree (이진 트리)
- Tree의 종류 중 1개
- 특징: 모든 노드들이 2개 이하의 자식을 가진다.

Binary Tree의 종류
1. Full Binary Tree (정 이진트리)
- 모든 노드가 0 or 2개의 자식 노드를 가짐.
2. Complete Binary Tree (완전 이진 트리)
- 마지막 Level을 제외하고 모든 레벨이 꽉 채워져 있음
- 마지막 Level이 꽉 채워져 있지 않으면, 왼쪽부터 채워져 있어야 함. (일반적인 견해)
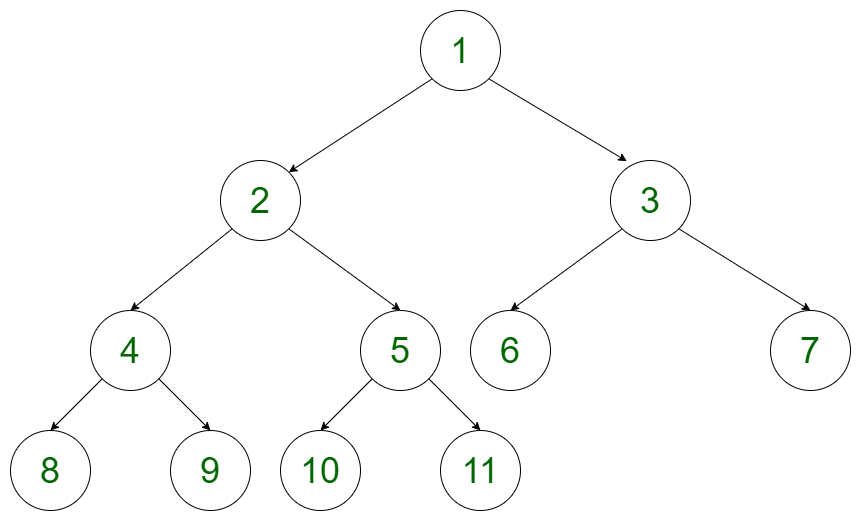
< '컴퓨팅 사고력을 기르는 이산수학 개정 3판' , 한빛아카데미 >
완전 이진 트리
- 높이가 h일 때, 레벨 0부터 h-1까지의 모든 부모노드의 차수가 2이고, 레벨 h는 레벨 h-1의 왼쪽부터 노드가 2개씩 채워져 있는 트리 (일부 관점에서의 견해)
(밑의 사진의 경우, 위 책에선 완전 이진 트리라고 보지 않는다.)

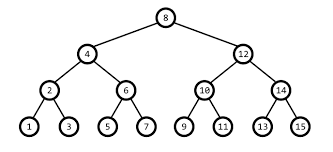
3. Perfect Binary Tree (포화 이진 트리)
- 정 이진트리 + 완전 이진 트리
- 모두 2개의 자식을 가지며, Left Subtree와 Right Subtree의 Level이 같다.
4. Balanced Binary Tree
- AVL Tree와 Red-Black Tree가 있음
- | H(Left) - H(Right) | <= k (k는 보통 1)
AVL Tree (노드 옆의 숫자는 Balance Factor)

Red-Black Tree

Q. 이진 트리의 임의의 레벨 i에서 최대로 갖을 수 있는 노드 수는?
- 최대 노드수: 2^i 개
Q. 높이가 h인 이진 트리가 갖을 수 있는 최대 노드 수는?
(단, h를 루트 노드에서 Leaf 노드에 이르는 가장 긴 path에 있는 간선의 수로 정의할 경우)
- <높이가 h인 (E 기준) 포화 이진트리의 최대 노드 수는?> 과 같은 질문
- 레벨이 h 일 때, 노드 수를 N(h)라 설정
- h=0 일 때, N(0) = 2^0 = 1
- h=1 일 때, N(1) = 2^0 + 2^1 = 3
- h=2 일 때, N(2) = 2^0 + 2^1 + 2^2 = 7
- h=3 일 때, N(3) = 2^0 + 2^1 + 2^2 + 2^3 = 15
- .
- .
- .
- h = n 일 때, N(n) = 2^0 + 2^1 + 2^2 +...+2^n
따라서 높이가 h 일 때, (이진 트리가 갖을 수 있는 최대 노드의 수) = (초항이 1이고 공비가 2인 등비수열의 합과 동일)
- N(max) = 2^(h+1) - 1
Q. 포화 이진 트리의 노드 수가 n이라면, Tree의 높이(h)는?
- 트리의 높이를 h라 하면, n = 2^(h+1) -1
- h에 대해서 정리하면, 2^h = (n+1) / 2
h = log2 (n+1) (2는 밑, (n+1)은 진수)
- h = log2 (n+1) (2는 밑, (n+1)은 진수)
Q. Maximum height를 갖는 트리 형태는?
(= n개의 노드를 갖는 트리들 중 height가 가장 큰것은?)

- 트리 중 불균형 이진 트리인 경우 -> h = n-1
'Python > 자료구조, 알고리즘' 카테고리의 다른 글
| 자료구조, 알고리즘) Graph - About Graph, DFS, BFS (1) | 2024.05.22 |
|---|---|
| 자료구조, 알고리즘) Sorting - Shellsort, Mergesort, Heapsort, Radixsort (1) | 2024.05.17 |
| 자료구조, 알고리즘) Sorting - Bubblesort, Selectionsort, Insertionsort, Quicksort + Partition (1) | 2023.12.10 |
| 자료구조) Binary Search Tree (6) | 2023.12.05 |
| 자료구조) Tree의 기본 개념 (3) | 2023.11.28 |