Shellsort (쉘 정렬)
- 데이터를 일정한 간격(gap)에 의해 여러 개의 부분 집합으로 나누기
- 삽입정렬이 부분적으로 정렬된 리스트에서 시간이 덜 걸린다는 것에서 착안한 정렬
- Insertionsort(삽입정렬)를 일정한 gap에 의해 실행
- Not stable, In-place 정렬 (추가 메모리X)
- 시간복잡도: 일반적으로 O(n^1.5) (gap sequenc에 따라 다름)
최악의 경우: O(n^2) - 역순 정렬, 최선의 경우: O(n) - 정렬된 입력, 원소가 모두 같은 입력
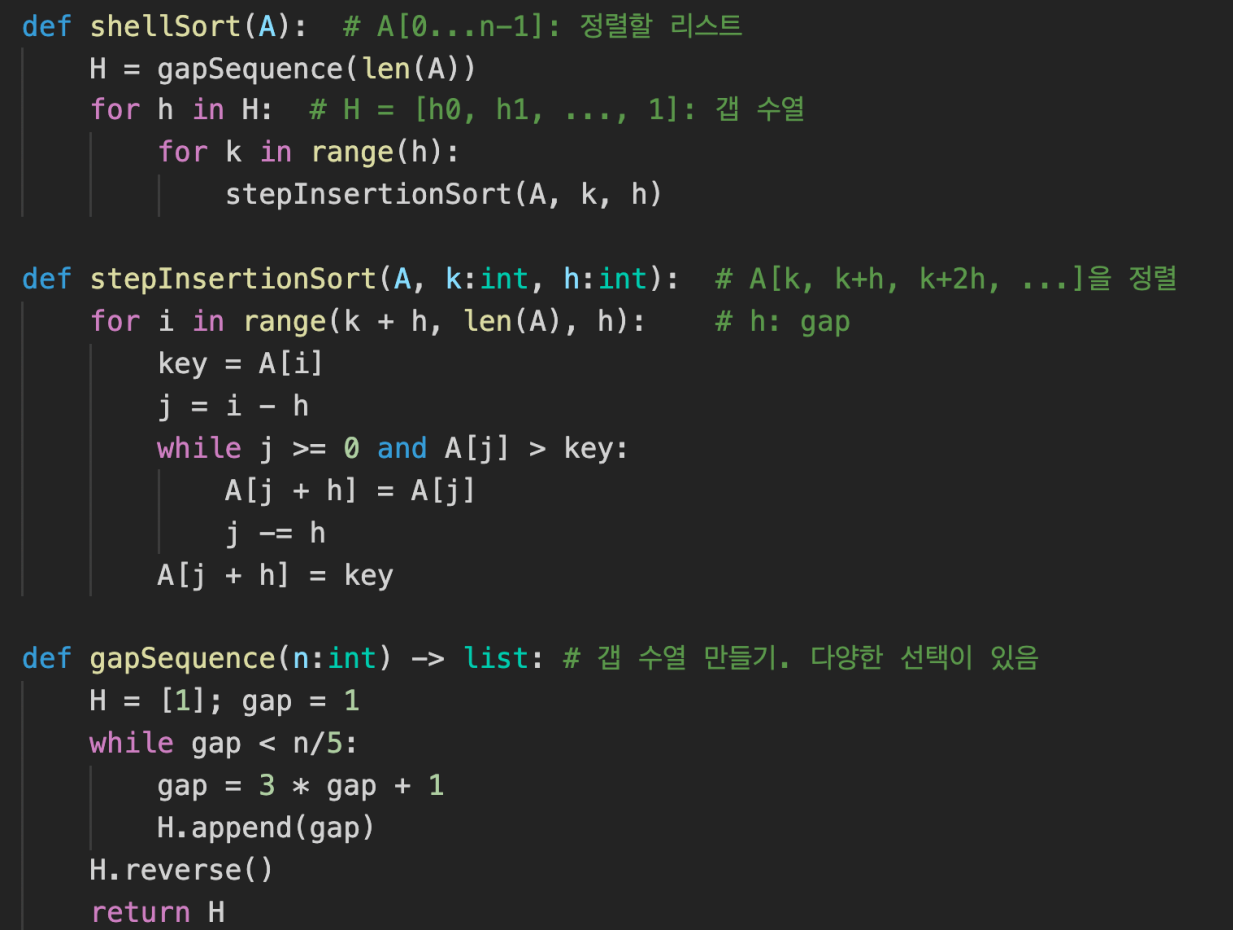
Shellsort Visualization

Shellsort Code with Python
더보기

출처: 학교 강의자료
Mergesort (병합정렬 or 합병정렬)
- Divide & Conquer : 분할 후 부분배열을 정렬
- Merge: 정렬된 부분배열들을 정렬
- 배열을 log N번 만큼 Divide하고 n개의 원소들을 비교연산 -> 최선 최악 평균 모두 O(n log n)
- In-place X, Stable O - O(n)의 공간복잡도가 필요
- 단점: 입력의 사이즈가 클 경우, 시간이 오래걸림
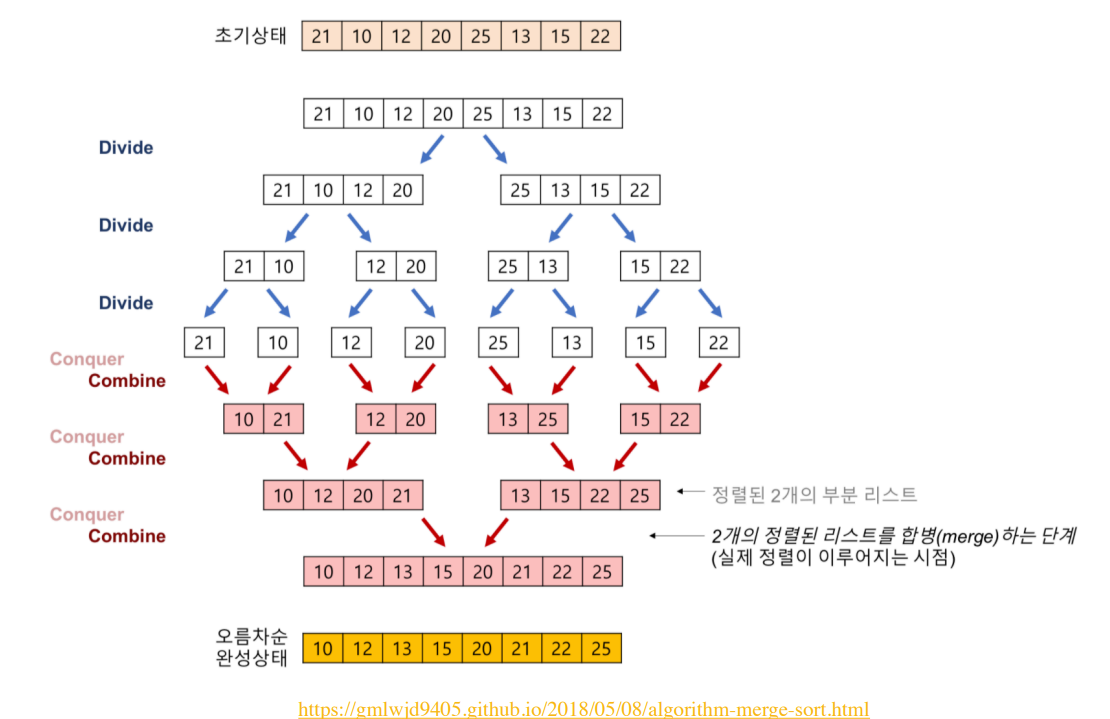
Mergesort Visualization
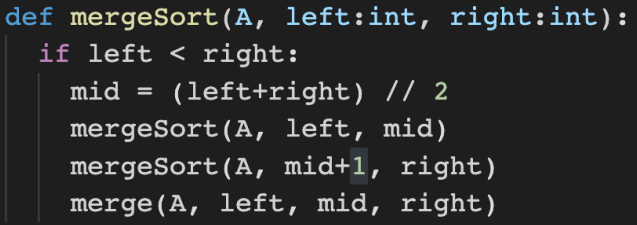
Mergesort Code with Python
더보기

출처: 학교 강의자료


Heapsort (힙 정렬)
- 힙 자료구조를 통한 정렬
- 시간 복잡도 - O(n log n) (최선, 최악, 평균 모두 동일)
- Stable, In-place 정렬
- 힙 정렬의 과정
더보기
1.입력을 buildHeap 알고리즘을 통해서 Heap 자료구조 구현
2, 루트값(max)과 마지막 원소 swap
3. Percolate-down (heapify down)과정을 통해 heap제작
4. 과정 반복
Heapsort visualization
- https://www.youtube.com/watch?v=H5kAcmGOn4Q&t=29s
Heapsort Code with Python
더보기
def heapSort(A):
buildHeap(A)
for last in range(len(A)-1, 0, -1): # n-1 번 반복
A[last], A[0] = A[0], A[last] # 루트 값 (즉 ,A[0]과 마지막 값 A[last]와 swap)
percolateDown(A, 0, last-1)
def buildHeap(A): # 리스트 A[0...len(A)-1]을 힙으로 만든다
for i in range((len(A)-2) // 2, -1, -1):
percolateDown(A, i, len(A)-1)
# A[k]를 루트로 하는 서브 트리가 A[k...end] 범위 내에서 힙 특성을 만족하도록 수선
# 주어진 조건: A[k]의 두 자식을 루트로 하는 서브 트리는 힙 특성을 만족함
def percolateDown(A, k:int, end:int):
child = 2*k+1 # 왼자식
right = 2*k+2 # 오른자식
if child <= end:
if right <= end and A[child] < A[right]:
child = right
# child: A[2k+1]와 A[2k+2] 중에 큰 원소의 인덱스
if A[k] < A[child]:
A[k], A[child] = A[child], A[k]
percolateDown(A, child, end)
코드 출처: 학교 강의자료
Radixsort (기수정렬)
- 다른 정렬과 다르게 숫자들의 자릿수로 비교 (일의 자리는 일의 자리끼리, 십의 자리는 십의 자리끼리)
- 시간복잡도 - O(dn) (d: 최대인 수의 자릿수, 일반적으로 10이하)
- 공간복잡도 - O(n) (최대 10개의 공간이 필요 0부터 9까지)
- In-place X, Stable O - 자릿수를 정렬하기 위해서 추가 메모리가 필요함
Radixsort Visualization
Radixsort Code with Python
이전에 정리했던 Sorting Algorithm들
2023.12.10 - [자료구조] - Sorting (bubblesort, selectionsort, insertionsort, quicksort + partition)
'Python > 자료구조, 알고리즘' 카테고리의 다른 글
| 자료구조, 알고리즘) Graph - Spanning Tree, MST, Kruskal, Prim (3) | 2024.05.22 |
|---|---|
| 자료구조, 알고리즘) Graph - About Graph, DFS, BFS (1) | 2024.05.22 |
| 자료구조, 알고리즘) Sorting - Bubblesort, Selectionsort, Insertionsort, Quicksort + Partition (1) | 2023.12.10 |
| 자료구조) Binary Search Tree (6) | 2023.12.05 |
| 자료구조) Binary Tree (4) | 2023.11.28 |